Noam Chomsky is a celebrity in many fields. Some translators get surprised when I mention that he is also well known in Computer Science. He invented (discovered?) a classification of grammars as formal systems according to their power of expression (or processing): the Chomsky Hierarchy.
This scheme classifies the languages generated by the grammars in four categories:
- Regular
- Context-free
- Context-sensitive
- Recursively enumerable
To each of them there is an automaton that can recognize sentences in the language:
- Finite automata, also known as Finite State Machines
- Pushdown automata
- Linear bounded automata
- Turing machines
Natural languages belong to the most powerful types of grammar, and the machine that corresponds to them is the Turing Machine.
I now present an example of a regular language, the simplest kind, to illustrate this striking correspondence between grammars and machines. Consider this grammar.
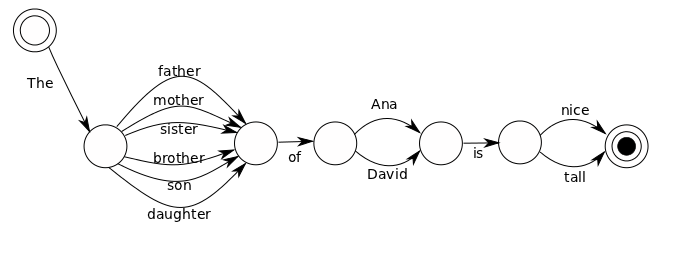
SENTENCE-> "The" KINDSHIP "is" ADJECTIVE KINDSHIP-> RELATION "of" PERSON RELATION-> "mother" | "father" | "sister" | "brother" | "son" | "daughter" PERSON-> "Ana" | "David" ADJECTIVE-> "nice" | "tall"
With it, we are able to build sentences as inspiring as “The mother of Ana is nice” and “The daughter of David is tall”.
The corresponding Finite State Machine recognizes these two sentences, plus the other 22 that can be constructed with it (writing them down is left as an amusing exercise to the reader). It consists of a number of states joined by labeled arrows representing transitions from one state to another. There is a special initial state, and another special final state:
It would be very easy at this point to get confused, and think that “finite” in Finite State Machine refers to the fact that only a finite number of sentences can be produced or recognized by them. This is not at all the case. It refers to the fact that there is a finite number of states (the circles, seven in this case). Making a slight modification of our grammar we would be able to build sentences of arbitrary length, even if the number of states is left unchanged.
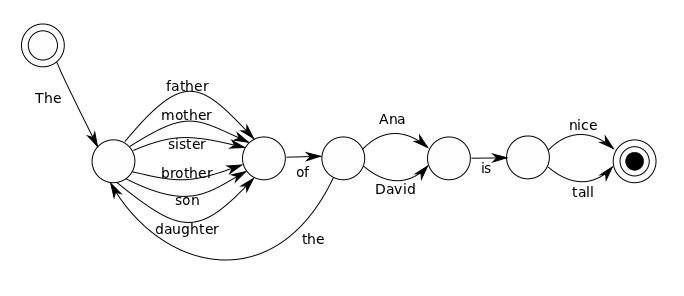
SENTENCE-> "The" KINDSHIP "is" ADJECTIVE KINDSHIP-> RELATION "of" PERSON RELATION-> "mother" | "father" | "sister" | "brother" | "son" | "daughter" PERSON-> "Ana" | "David" | "the" KINDSHIP ADJECTIVE-> "nice" | "tall"
We have added “the” KINDSHIP as one alternative more for PERSON. In the Finite State Machine it appears simply as a new arrow going back to the second state.
Now we can build up sentences such as “The son of the sister of the mother of the daughter of David is tall”. I used to play this game with my ex-friends (they become automatically ex-friends the moment I start playing this game with them). When talking about my brother, for example, I’d refer to him as the son of the auntie of the sister of my cousin.
The Chomsky Hierarchy has been extensively studied from both ends. In Computer Science they provide the foundations of syntax for programming languages, among many other things. And many work has been put into trying to capture the structure of real languages like English with grammars and their corresponding machines for many purposes, among them translation. Translation systems based in this approach are known as “rule based”.